Code
if (!require("pacman")) install.packages("pacman")Loading required package: pacmanCode
pacman::p_load(haven, DescTools, knitr, kableExtra, ineq, ggplot2, formatdown, tidyverse, WDI)ECON 4643: Development Economics
Lecture 4: Module 1-Growth
Reading
ED Ch 3
Introduction
At the macro level, successful development requires a combination of:
Reduction in inequality
Reduction poverty and vulnerability
Economic growth
We now turn to economic growth (after having discussed inequality and poverty in Lectures 2 and 3)
Definition
Economic growth is:
The rate of increase in a country’s average income.
Total income equals the total value of production, so the rate of economic growth rate is positive when aggregate labor productivity is rising.
Economic growth is usually measured as the average annual rate of growth in real per capita gross domestic product (GDP).
Economic Growth and Development
Economic growth is necessary for development
But economic growth is not sufficient for full development success
Reading Assignment (on Canvas): Easterly, W (2001) ``The Political Economy of Growth Without Development: A Case Study of Pakistan’’
Growth Patterns
Historical growth experience
Four-minute video in which statistician Hans Rosling provides a visual history of growth and development around the world over the last 200 years: http://www.flixxy.com/200-countries-200-years-4-minutes.htm
Determinants of Growth
Proximate Sources: The kinds of change in socioeconomic activity that give rise to economic growth and the related choices through which those changes come about.
- Example: trade
Economic determinants: The types of policies, institutions, external market conditions, and other circumstances that are taken as given by people within the socioeconomic system, and that affect how willing and able people are to make the choices associated with the proximate sources of growth
- Example: rule of law
Political determinants: The political conditions that lead policymakers to put good policies and institutions into place
- Example: Accountability of political leaders
Proximate Sources of Growth: Firm Level
Economic growth involves growth in aggregate labor productivity.
Economists begin their study of productivity by thinking about the many firms throughout the economy in which production takes place.
Economists organize their thinking about the technological possibilities a firm faces around the concept of a production function.
Production function
- A production function describes how the maximum quantity of output the firm could produce is related to the quantities of production factors it employs.
\[ Y = F\left(L, K; A\right) \]
Where \(Y\) is output quantity \(L\) is labor \(K\) is capital \(A\) represents total factor productivity
Definitions
We will make frequent reference to the following - the average product of labor \[AP_L = \frac{Y}{L} = \frac{F\left(L, K; A\right)}{L} \]
- the average product of capital
\[AP_K = \frac{Y}{K} = \frac{F\left(L, K; A\right)}{K} \]
- the marginal product of labor \[
MP_L = \frac{\partial F\left(L, K; A\right) }{\partial L}
\] or \(\frac{\Delta Y}{\Delta L}\)
the marginal product of capital \[ MP_L = \frac{\partial F\left(L, K; A\right) }{\partial K} \] or \(\frac{\Delta Y}{\Delta K}\)
We expect:
- Positive but diminishing marginal product of \(L\)
- Positive but diminishing marginal product of \(K\)
- Positive function of \(A\)
Illustration: suppose that the production function is
\[ Y=4 L K+0.1 L^2 K+0.2 L K^2-0.04 L^3 K-0.02 L K^3 \] In this case, the average product of labor is
\[ \text{APL} = \frac{Y}{L} = 4K + 0.1LK + 0.2LK^2 - 0.04L^2K -0.02K^3 \] and the marginal product of labor is
\[ \text{MPL} = \frac{\partial Y}{\partial L} = 4K + 0.2LK + 0.2K^2 - 0.12LL^2K - 0.02K^3 \] The R-chunk below will take a value of capital \(K\), the maximum size of labor \(n\) and a technology shifter \(A\), and then generate a table of output (Table 1), and average and marginal products.
Code
production_data <- production_function(K = 3, n = 15, A=5)
#print(production_data)
kable(production_data)| Labor | Capital | Output | APL | MPL |
|---|---|---|---|---|
| 0 | 3 | 0.00 | NA | 1.26 |
| 1 | 3 | 16.44 | 16.44 | 6.50 |
| 2 | 3 | 32.76 | 16.38 | 11.02 |
| 3 | 3 | 48.24 | 16.08 | 14.82 |
| 4 | 3 | 62.16 | 15.54 | 17.90 |
| 5 | 3 | 73.80 | 14.76 | 20.26 |
| 6 | 3 | 82.44 | 13.74 | 21.90 |
| 7 | 3 | 87.36 | 12.48 | 22.82 |
| 8 | 3 | 87.84 | 10.98 | 23.02 |
| 9 | 3 | 83.16 | 9.24 | 22.50 |
| 10 | 3 | 72.60 | 7.26 | 21.26 |
| 11 | 3 | 55.44 | 5.04 | 19.30 |
| 12 | 3 | 30.96 | 2.58 | 16.62 |
| 13 | 3 | -1.56 | -0.12 | 13.22 |
| 14 | 3 | -42.84 | -3.06 | 9.10 |
| 15 | 3 | -93.60 | -6.24 | 4.26 |
Code
# Plot APL and MPL against Labor using ggplot2
ggplot(production_data, aes(x = Labor)) +
geom_line(aes(y = APL, colour = "APL"), size = 1) + # Plot APL
geom_line(aes(y = MPL, colour = "MPL"), size = 1) + # Plot MPL
labs(title = "APL and MPL against Labor",
x = "Labor",
y = "Productivity",
colour = "Measure") +
scale_colour_manual(values = c("APL" = "blue", "MPL" = "red")) +
theme_minimal()
Increasing capital
Now, we can explore what happens if we increase capital from \(K=3\) to \(K=6\).
Code
production_data_K6 <- production_function(K = 6, n = 15, A=5)
# Plot APL and MPL against Labor for both K = 10 and K = 15 using ggplot2
ggplot() +
geom_line(data = production_data, aes(x = Labor, y = APL, colour = "APL K=3"), size = 1) +
geom_line(data = production_data, aes(x = Labor, y = MPL, colour = "MPL K=3"), size = 1) +
geom_line(data = production_data_K6, aes(x = Labor, y = APL, colour = "APL K=6"), size = 1, linetype = "dashed") +
geom_line(data = production_data_K6, aes(x = Labor, y = MPL, colour = "MPL K=6"), size = 1, linetype = "dashed") +
labs(title = "APL and MPL against Labor for K=3 and K=6",
x = "Labor",
y = "Productivity",
colour = "Measure") +
scale_colour_manual(values = c("APL K=3" = "blue", "MPL K=3" = "red", "APL K=6" = "darkblue", "MPL K=6" = "darkred")) +
theme_minimal()
Proximates Sources of Growth
The discussion of firms suggests that at the aggregate level, average labor productivity can grow through:
Accumulation of physical capital (more rapid than the rate of growth of population)
Accumulation of human capital (increasing average skill level of workforce)
Improvements in technology (through research, development, dissemination, purchase and adoption of new technologies)
Improvements in technical efficiency
At the aggregate level, average labor productivity may also grow through re-allocations of labor across activities that:
Shift labor from sectors or firms where the value of the marginal product of labor (VMPL) is lower to sectors or firms where the VMPL is higher
Shift labor out of unemployment into employment
Shift labor out of rent-seeking activities into productive activities
Proximates Sources of Growth: Aggregate Level
Accumulation of assets
Physical capital
- Machinery, inventory
- Infrastructure
Human capital
Improvements of technology
Improved efficiency in utilsation of assets
- Shifting labor from less to more productive uses
- between sectors, between firms
- Reducing waste
- reducing corruption
- reducing “rent seeking”
- reducing unemployment
- Shifting labor from less to more productive uses
Growth accounting studies seek to quantify the relative importance of factor accumulation (i.e. rising quantities of physical or human capital per worker) and growth in total factor productivity (i.e. all other proximate sources of growth) for explaining historical growth.
Often they find that factor accumulation and TFP growth each explain about half of overall growth.
Development accounting studies seek to quantify the relative importance of differences in physical or human capital per worker and differences in TFP for explaining differences across countries in GDP per worker.
Often they find that differences in capital per worker and differences in TFP each explain about half of the cross-country differences.
Empirical observations suggest that developing countries have room to improve in all of these areas.
- Physical capital per worker
- Human capital per worker
- Level of technology
- Technical efficiency
- Efficiency in allocation of labor across sectors and firms
- Unemployment and under-employment
- Rent-seeking and other wasteful activities
Determinants of Growth: Macro Perspective
Why do capital accumulation, technical change, improvements in efficiency and reductions in waste happen more rapidly in some countries than others?
Determinants considered in cross-country growth regression literature:
- Current policy (openness to international trade, fiscal discipline)
- Geography (distance from equator, landlocked)
- Long-lasting social characteristics (languages, religions)
- Legacy of earlier policies (education stock)
- Institutional heritage (colonizers, legal systems)
- Current institutions beyond codified policies (property rights, corruption, bureaucracy)
Growth Models
Growth Rates
- The growth rate of a variable \(w\), between time periods \(t_0\) and \(t_1\) is: \[ \dot{w} = \frac{w_{t_{1}}-w_{t_{0}}}{w_{t_{0}}} = \frac{\Delta w}{w_{t_{0}}} \]
- We can drop the time subscript \(t\), to have:
\[ \dot{w} = \frac{\Delta w}{w} \] - Note the following rules of growth rates:
- The growth rate of \(wz\) is:
\[ \frac{\Delta w}{w} + \frac{\Delta z} {z} \]
- The growth rate of \(\frac{w}{z}\) is:
\[ \frac{\Delta w}{w} - \frac{\Delta z} {z} \]
- For example, if GDP is \(Y\) and population is \(N\), the the growth rate of GDP per capita \(\left( \frac{Y}{N}\right)\) is \(\dot{Y} - \dot{N}\), where \(\dot{Y} = \frac{\Delta Y}{Y}\) and \(\dot{N} = \frac{\Delta N}{N}\)
Average Growth Rates
- We are often interested in the average growth rate over \(T\) time periods, let say years. In this case, we are assuming a constant growth rate \(G\) over the \(T\) periods. Suppose we observe GDP per capita of a given country in year \(0\) (\(y_0\)) and year \(T\) (\(y_T\). Constant growth implies that: \[ y_T = y_0 \left(1 + G \right)^{T} \]
- We solve for \(G\) as:
\[ G = \left( \frac{y_T}{y_0} \right)^{\frac{1}{T}} - 1 \] -This is easily calculated with a handheld calculator.
- I one assumes that time is continuous, then the growth rate \(g\) satisfies \(y(t) = y(0)e^{gt}\), and we can solve for \(g\) as:
\[ g = \frac{ln y(t) - ln y(0)}{t} \]
- If the growth rate is small enough, then
\[ G \simeq \frac{ln\frac{y_t}{y_0}}{t} = g \]
Doubling Time
If given the growth rate, we can estimate how long it would take for the vatiable to double (or triple, etc.)
With discrete time, we know that: \[ 1 + G=\left(\frac{y_T}{y_0}\right)^{\frac{1}{T}} \]
Take the natural log of both sides and solve for \(T\)
GDP doubling means that \(\frac{y_T}{y_0} = 2\), so we can substitute to get
\[ T = \frac{ln(2)}{ln (1 + G)} \simeq \frac{0.6931}{ln(1+ G)} \]
- if \(G\) is given, this formula is easy to evaluate.
The Basic Growth Model
The basic growth model is based on five equations:
Aggregate production function \(Y = F(K, L)\)
Saving \(S\) depends on income \(Y\), and \(s\), i.e. \(S=s Y\). Example: if \(s=.20\) and \(Y=10\) billions, then saving is \(S=2 B\)
- \(s\) is called the marginal propensity to save, i.e. how many cents are saved out of each dollar. You can see that \(s = 1-c\), where \(c\) is the propensity to consume.
Investment \(I\) is funded with saving; \(\mathrm{S}=\mathrm{I}\) (Saving=Investment)
Change in \(\Delta \mathrm{K}=(\mathrm{I}-\mathrm{dK})\) where \(\mathrm{d}=\) depreciation and \(\mathrm{K}=\) capital
Change in \(\Delta \mathrm{L}=\mathrm{nxL} \mathrm{n}=\) population growth and \(\mathrm{L}=\mathrm{Labor}\) force, If \(\mathrm{L}=1\) mill. & \(\mathrm{n}=.02\)
Combining 2,3,4, leads to \(\Delta \mathrm{K}=\mathrm{sY}-\mathrm{dK}\)
5 equations and 5 variables can be solved and the change in \(\mathrm{K}\) can be substituted into Production function \(\mathrm{Y}=\mathrm{f}(\mathrm{K}, \mathrm{L})\)
The Harrod-Domar Growth Model
The HD Growth model is a particular model with basic feature of fixed coefficient production function.
It assumes no substitution between labor and capital \(\mathrm{Q}= F\left( K, L \right) = \min \mathrm{F}(\mathrm{L}, \mathrm{K})\) : the production Isoquant is L shaped
- Labor and capital are perfect complements
It also shows constant returns to scale (CRS) i.e. doubling inputs will double output as you can see in Figure 3
Code
# Adjust the Leontief production function to Y = min(K, L)
hdpf <- function(K, L) {
pmin(K, L)
}
# Generate a grid of K and L values
K_range <- seq(0, 50, length.out = 100)
L_range <- seq(0, 50, length.out = 100)
# Create a dataframe for plotting
grid <- expand.grid(K = K_range, L = L_range)
grid$Y <- with(grid, hdpf(K, L))
# Isoquant levels for specific combinations
Y1 <- hdpf(10, 20)
Y2 <- hdpf(20, 40)
# Base plot
p <- ggplot(grid, aes(x = K, y = L)) +
geom_contour(aes(z = Y, colour = factor(stat(level))), breaks = c(Y1, Y2)) +
scale_colour_manual(values = c('blue', 'red'),
name = "Isoquant",
labels = c("Isoquant I (K=10, L=20)", "Isoquant II (K=20, L=40)")) +
labs(title = "HD Production Function Isoquants: Y = min(K, L)",
x = "Capital (K)", y = "Labor (L)") +
theme_minimal() +
coord_fixed(ratio = 1) # Ensure the same scale for both axes
# Print the plot
print(p)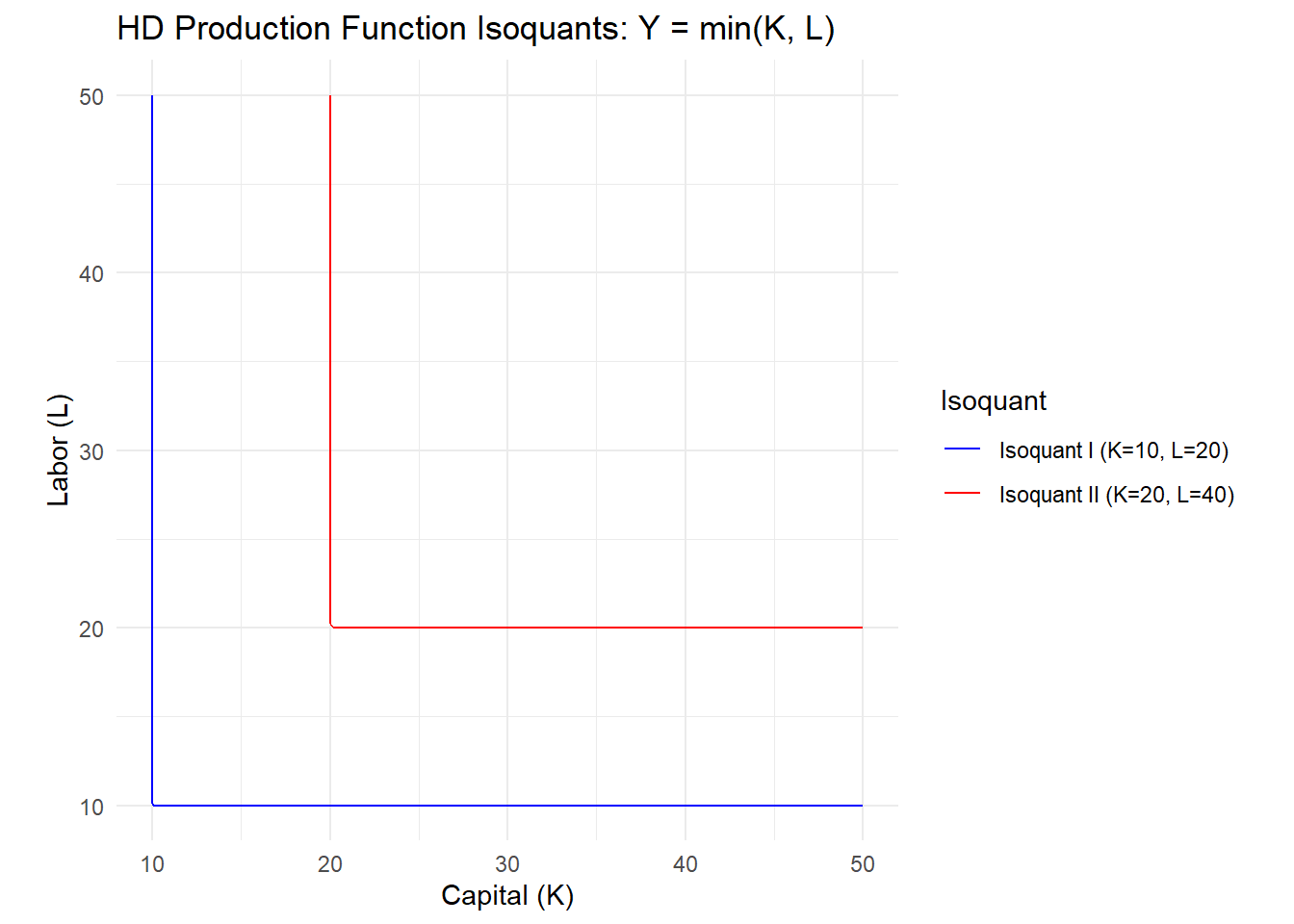
Growth Rate from the HD Model
Let \(Y\) (income) be GDP and \(S\) be savings. The level of savings is a function of the level of GDP as before, say \(S = sY\).
The level of capital \(K\) needed to produce an output \(Y\) is given by the equation \(K = vY\), where \(v\) is the incremental capital-output ratio (ICOR), and \(v = \frac{K}{Y}\)
- The ICOR is a measure of the productivity of capital or investment
From \(K = vY\), we get \(\Delta K = v \Delta Y\)
From equation 4 above, \(\Delta \mathrm{K}=\mathrm{I}-\mathrm{dK}\)
Combining (a) and (b), we get:
Notice that the left hanside term of the last equation is just the growth rate of \(Y\) (GDP). Thus, in the basic HD model, the growth rate is \(Y_g = \left(\frac{s}{v}\right) - d\)
The policy prescription of the model is straightforward: promote saving to accelerate growth.
Numerical illustration
Suppose that the propensity to consume is \(c = 0.76\). The capital (\(K\)) stock is \(3,000\) units, GDP (\(Y\)) is \(1,000\), and the depreciation rate (\(d\)) is \(0.05\). What is the growth rate of this economy?
- We can find \(s = 1 - 0.76 = 0.24\), \(v = \frac{3000}{1000} = 3\), and us the growth equation \[Y_g = \frac{0.24}{3} - 0.05 = 0.03\]
- The growth rate of this economy is \(3\%\), based on HD growth model.
Growth rate of income per capita from HD model
- Let \(g(x\)) be the growth rate of \(x\), so that \(g(\frac{w}{z})\) is the growh the rate of \((\frac{w}{z})\):
- \(g(\frac{w}{z}) = g(w) - g(z)\)
- Income per capita is: \(\frac{Y}{N}\), where \(N\) is the population. Growth of income per capita is:
- \(g(\frac{Y}{N}) = g(Y) = g(N)\)
- Let \(y\) be income per capita, and \(n\) be population growth. We know \(g(Y)\), i.e. \(Y_g\).
- Per capita income growth is:
- \[y_g = \frac{s}{v} - (d+n)\]
- In this model, every 1% increase in the population growth rate translates into a 1% fall in the growth rate of per capita income
- Saving rate enhances growth in per capita income, while depreciation rate and population growth rate reduce growth
- Can have a Malthusian trap when \(n > \frac{s}{v}- d\)
Code
countries <- c("KE", "MX", "CN", "CI", "VN") # ISO2 country codes
indicators <- c(GFCF = "NE.GDI.FTOT.ZS", GDP_Growth = "NY.GDP.MKTP.KD.ZG")
# Fetch data for 2010 and 2019
wdi_data <- WDI(indicator = indicators, country = countries, start = 2010, end = 2019, extra = FALSE)
# Calculating averages for each indicator across 2015 to 2020 for each country
avg_data <- wdi_data %>%
group_by(country) %>%
summarize(GFCF_Percent_GDP = mean(GFCF, na.rm = TRUE),
GDP_Annual_Growth_Percent = mean(GDP_Growth, na.rm = TRUE)) %>%
mutate(ICOR = GFCF_Percent_GDP/GDP_Annual_Growth_Percent)
knitr::kable(avg_data,
format = "html",
col.names=c("Country", "Gross fixed capital formation (% of GDP)", "GDP growth (annual %)", "ICOR"),
digits = 2,
full_width = F, position = "float_top",
format.args = list(big.mark = "," , scientific = FALSE))%>%
footnote(c("Source: World Bank, World Development Indicators", "Adapted from de Janvry and Sadoulet (2021), Table 8.1"))| Country | Gross fixed capital formation (% of GDP) | GDP growth (annual %) | ICOR |
|---|---|---|---|
| China | 43.16 | 7.68 | 5.62 |
| Cote d'Ivoire | 21.13 | 6.24 | 3.39 |
| Kenya | 20.72 | 5.03 | 4.12 |
| Mexico | 22.82 | 2.34 | 9.77 |
| Viet Nam | 30.24 | 6.58 | 4.60 |
| Note: | |||
| Source: World Bank, World Development Indicators | |||
| Adapted from de Janvry and Sadoulet (2021), Table 8.1 |
The Solow Growth Model
Builds on the Harrod–Domar model
Adds several neoclassical features
- Decreasing marginal product to each factor of production
- Possibility of substitutions between labor and capital in production \(\Rightarrow\) countries choose
- a more labor-intensive growth path if labor is cheap (a low capital–labor ratio), or _ a more capital-intensive growth path if labor is expensive (a high capital–labor ratio)
Incorporates total factor productivity (TFP)
Maintains constant returns to scale assumption (Harrod–Domar)
Figure 4 show the isoquants of a Cobb-Douglas production function, with \(A=1\), and \(\alpha=1\)
Code
# Define the Cobb-Douglas production function
cobb_douglas_production <- function(K, L) {
K^0.5 * L^0.5
}
# Target output levels
Y_targets <- c(10, 20)
# Generate a grid of K and L values
K_range <- seq(1, 50, length.out = 100) # Start from 1 to avoid division by zero
L_range <- seq(1, 50, length.out = 100)
# Create a dataframe for plotting isoquants
isoquants <- data.frame(K = numeric(), L = numeric(), Output = numeric(), Isoquant = factor())
# Calculate K and L combinations for each Y target
for (Y in Y_targets) {
for (K in K_range) {
L <- (Y / (K^0.5))^2
if (L <= 50) { # Include only the combinations within the specified L range
isoquants <- rbind(isoquants, data.frame(K = K, L = L, Output = Y, Isoquant = as.factor(Y)))
}
}
}
# Plot the isoquants
ggplot(isoquants, aes(x = K, y = L, colour = Isoquant)) +
geom_line() +
scale_colour_manual(values = c("10" = "red", "20" = "blue"),
name = "Output Level",
labels = c("Y = 10", "Y = 20")) +
labs(title = "Cobb-Douglas Production Function Isoquants",
x = "Capital (K)", y = "Labor (L)") +
theme_minimal() +
coord_fixed(ratio = 1) # Ensure the same scale for both axes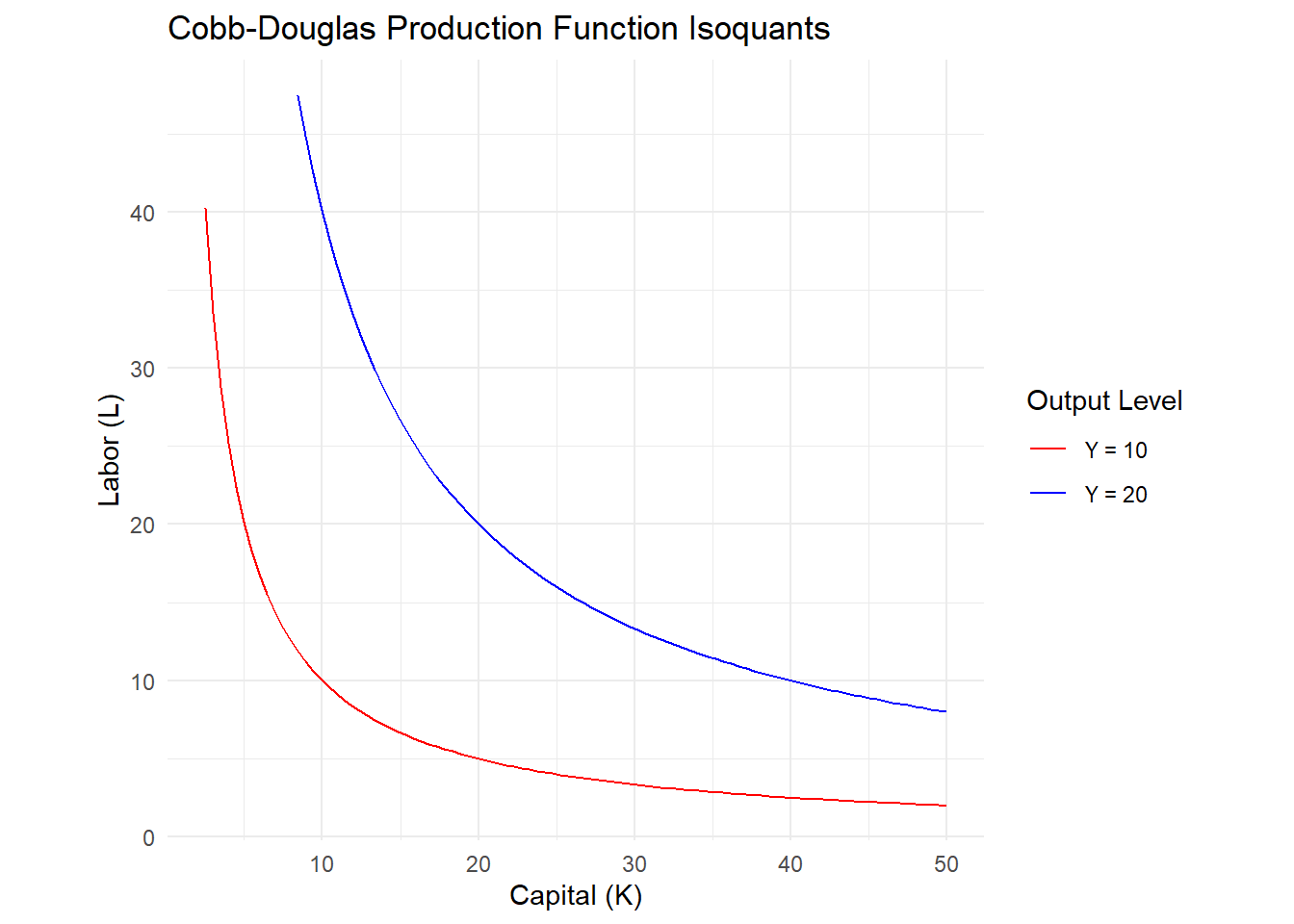
Code
# Define the per-worker production function
f_k <- function(k) {
k^0.5
}
# Generate a sequence of k values
k_values <- seq(0, 50, by = 0.1)
# Calculate y for each k
y_values <- f_k(k_values)
# Create a dataframe for plotting
data <- data.frame(k = k_values, y = y_values)
# Plot y as a function of k using ggplot
ggplot(data, aes(x = k, y = y)) +
geom_line(color = "blue") +
labs(title = "Per-worker Production Function: $y = k^0.5$",
x = "Capital per worker (k)",
y = "Output per worker (y)") +
theme_minimal()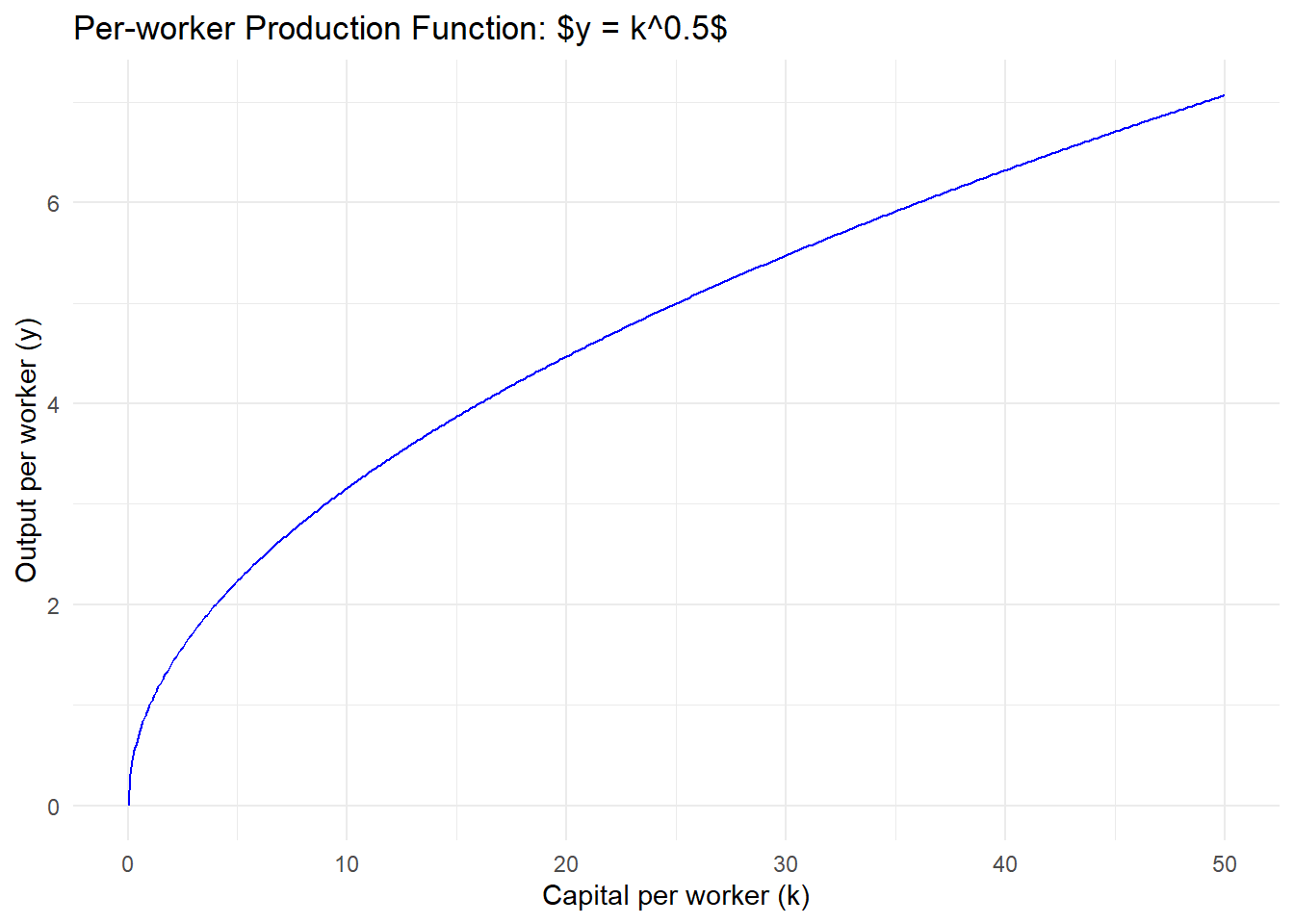
- Production Function:
- We start with the neoclassical (Cobb-Douglas) aggregate production function: \(Y\left(t\right) = A K(t)^{\alpha}L(t)^{(1-\alpha)}\) where:
- \(\mathrm{Y}(\mathrm{t})\) represents total output.
- \(\mathrm{K}(\mathrm{t})\) is the capital stock.
- \(\mathrm{L}(\mathrm{t})\) is the labor force.
- \(A\) represents total factor productivity.
- \(\alpha\) is the capital share in production (a constant between \(0\) and \(1\) ).
- Per Worker Terms:
- Define \(y=\frac{Y}{L}\) as output per worker.
- We have: \(y=A k^{\alpha}\) where \(k= \frac{K}{L}\) is capital per worker.
- Capital Accumulation Equation:
The change in capital is given by: $ K=s Y- d K $ where:
\(s\) is the saving rate.
\(d\) is the depreciation rate.
Key additional assumptions
- Constant saving rate
- Constant depreciation rate
- Derivation
The rest is basic algebra
Divide the capital accumulation equation by \(K\): $ = s - d $
\[ \frac{\Delta{K}}{K}=s \frac{Y}{K}-d=s \frac{\frac{Y}{L}}{\frac{K}{L}}-d=s \frac{y}{k}-d \]
Notice that: \[ \frac{\Delta{k}}{k}=\frac{\Delta{K}}{K}-\frac{\Delta{L}}{L}=\frac{\Delta{K}}{K}-n \Rightarrow \frac{\Delta{K}}{K}=\frac{\Delta{k}}{k}+n \]
We get:
\[ \frac{\Delta{k}}{k}+n=s \frac{y}{k}-d \Rightarrow \Delta{k}=s y-(d+n) k \]
- Finally, we get the fundamental differential Equation of Solow model: \[ \Delta {k}=s A k^\alpha-(d+n) k \]
- Steady State Analysis
Because, the Solow model is dynamic, it assumes that each country converges to its steady state, where capital stops growing, i.e. \(\Delta K = 0\).
\(0= \Delta {k^{\star}}=s A (k^{\star})^\alpha-(d+n) k\) \(\Rightarrow\)
The steady state capial per worker is: \[ k^*=\left(\frac{s A}{n+ d}\right)^{\frac{1}{1-\alpha}} \]
And the steady state output per worker is:
\[ y^*=\left(\frac{s A}{n+d}\right)^{\frac{\alpha}{1-\alpha}} \] - The steady state ouput per worker is increasing in the saving rate (\(s\)), and decreasing in the population growth rate (\(n\)) and the depreciation rate (\(d\)).
Code
import numpy as np
import matplotlib.pyplot as plt
# Adjusted parameters for the Solow model
n = 0.03 # population growth rate
d = 0.06 # depreciation rate
s = 0.2 # saving rate
s_prime = 0.4 # new saving rate
alpha = 0.3 # capital's share of income, for a Cobb-Douglas production function
k_max = 10 # maximum capital to plot
# Define the production function, for simplicity we assume a Cobb-Douglas production function
def f(k):
return k**alpha
# Create a grid of k (capital per worker) values
k = np.linspace(0.00, k_max, 200) # Start from 0.01 to avoid division by zero
# Calculate output per worker
y = f(k)
# Calculate investment (saving) per worker
sy = s * y
sy_prime = s_prime * y
# Calculate break-even investment level (depreciation plus population growth)
ndk = (n + d) * k
# Plot the Solow model
plt.figure(figsize=(10, 6))
# Plot the production function y = f(k)
plt.plot(k, y, label='y = f(k)', color='black')
# Plot the saving function s * f(k)
plt.plot(k, sy, label='sy', color='blue')
# Plot the (n+d)k line
plt.plot(k, ndk, label='(n+d)k', linestyle='--', color='grey')
# Add annotations for the steady state levels of capital
k_star = (s / (n + d))**(1 / (1 - alpha))
plt.axvline(x=k_star, color='blue', linestyle=':', linewidth=1)
# Add labels and title
plt.xlabel('Capital per worker, k')
plt.ylabel('Output, investment, and depreciation per worker')
plt.title('An Increase in the Saving Rate in the Solow Model')
# Add a legend
plt.legend()
# Show the plot with a grid
plt.grid(True)
plt.show()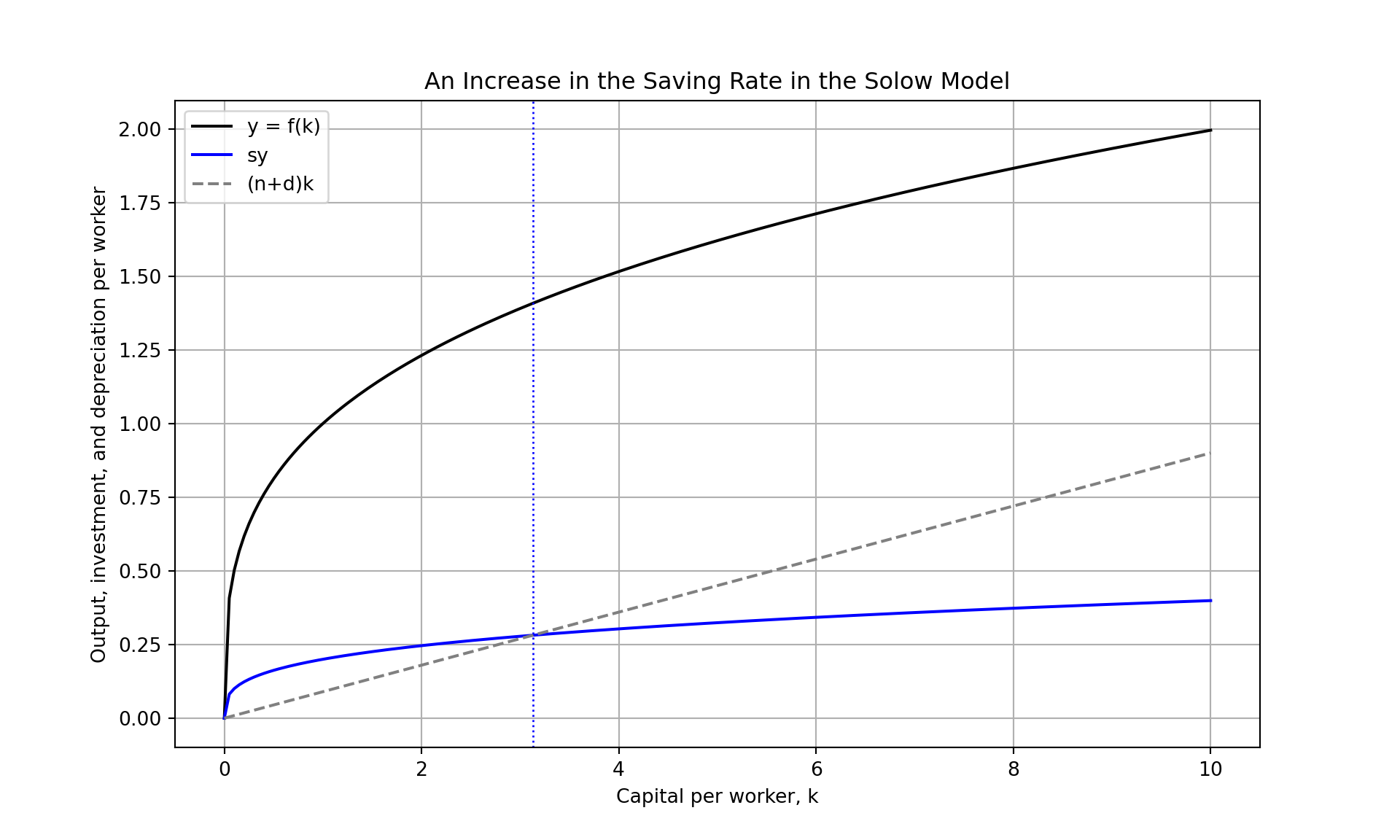
Code
import numpy as np
import matplotlib.pyplot as plt
# Adjusted parameters for the Solow model
n = 0.03 # population growth rate
d = 0.06 # depreciation rate
s = 0.2 # saving rate
s_prime = 0.4 # new saving rate
alpha = 0.3 # capital's share of income, for a Cobb-Douglas production function
k_max = 10 # maximum capital to plot
# Define the production function, for simplicity we assume a Cobb-Douglas production function
def f(k):
return k**alpha
# Create a grid of k (capital per worker) values
k = np.linspace(0.00, k_max, 200) # Start from 0.01 to avoid division by zero
# Calculate output per worker
y = f(k)
# Calculate investment (saving) per worker
sy = s * y
sy_prime = s_prime * y
# Calculate break-even investment level (depreciation plus population growth)
ndk = (n + d) * k
# Plot the Solow model
plt.figure(figsize=(10, 6))
# Plot the production function y = f(k)
plt.plot(k, y, label='y = f(k)', color='black')
# Plot the saving function s * f(k)
plt.plot(k, sy, label='sy', color='blue')
# Plot the new saving function s' * f(k)
plt.plot(k, sy_prime, label="s'y", color='cyan')
# Plot the (n+d)k line
plt.plot(k, ndk, label='(n+d)k', linestyle='--', color='grey')
# Add annotations for the steady state levels of capital
k_star = (s / (n + d))**(1 / (1 - alpha))
k_star_prime = (s_prime / (n + d))**(1 / (1 - alpha))
plt.axvline(x=k_star, color='blue', linestyle=':', linewidth=1)
plt.axvline(x=k_star_prime, color='cyan', linestyle=':', linewidth=1)
# Add labels and title
plt.xlabel('Capital per worker, k')
plt.ylabel('Output, investment, and depreciation per worker')
plt.title('An Increase in the Saving Rate in the Solow Model')
# Add a legend
plt.legend()
# Show the plot with a grid
plt.grid(True)
plt.show()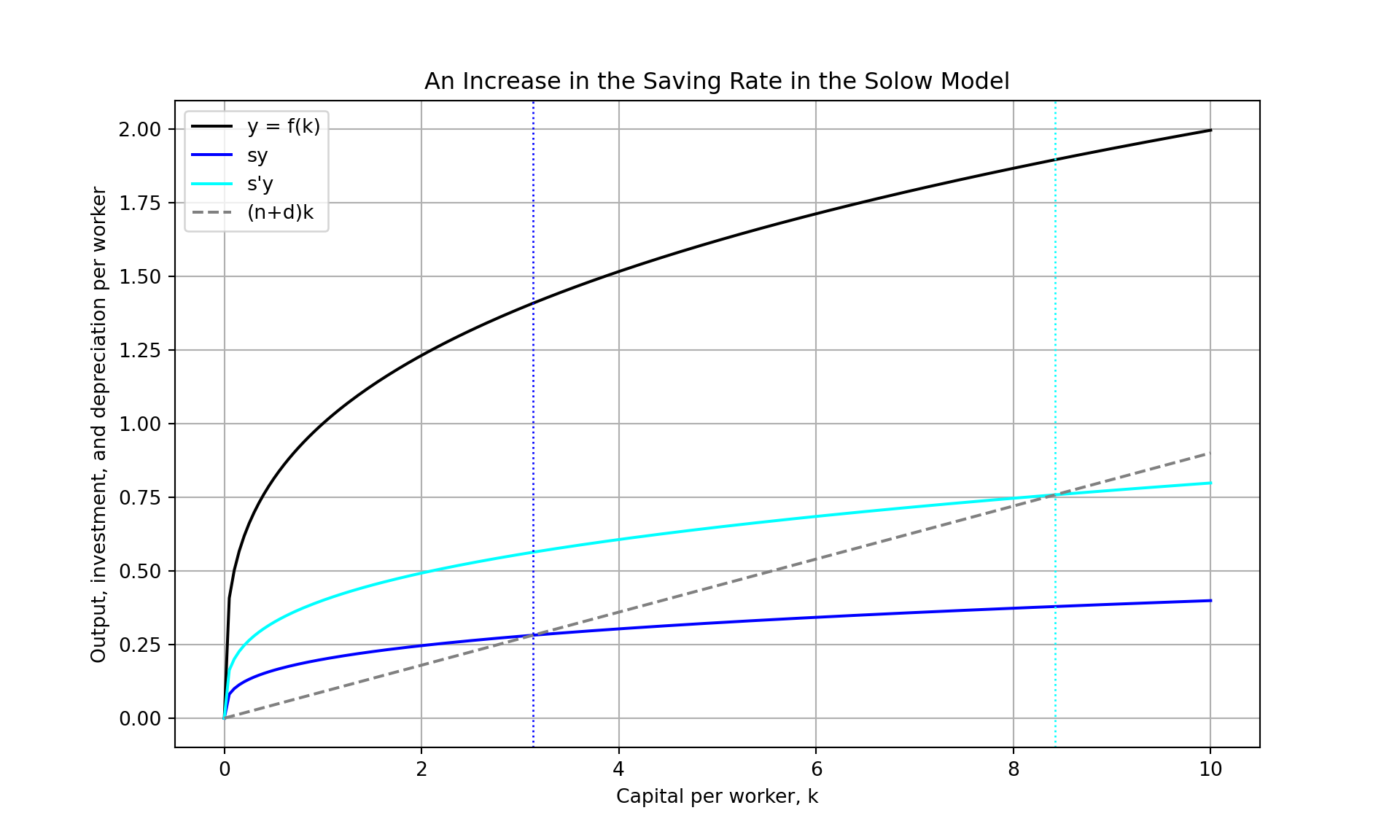
Evaluation the Solow Model
Why are some countries rich (have high per worker GDP) and others are poor (have low per worker GDP)?
Solow model: if all countries are in their steady states, then:
Rich countries have higher saving (investment) rates than poor countries
Rich countries have lower population growth rates than poor countries
Total Factor Productivity
- Use the Cobb-Douglas production function we started with, and drop the time subscript (\(t\)) for legibility
\[ Y = A K^{\alpha}L^{(1-\alpha)} \] - Using the growth rate formulas, the growth of \(Y\) is:
\[ \frac{\Delta Y}{Y} = \frac{\Delta A}{A} + \alpha \frac{\Delta K}{K} + \left(1-\alpha \right)\frac{\Delta L}{L} \] - This is called a growth accounting equation
- Total factor productivity is the part of of growth of \(Y\), wich is not explained by the growth of \(K\) and \(L\), i.e.
\[ \frac{\Delta A}{A} = \frac{\Delta Y}{Y} - \alpha \frac{\Delta K}{K} - \left(1-\alpha \right)\frac{\Delta L}{L} \]